6.25

In Section 6.9.4, we represented a ternary relationship (repeated in Figure 6.29a) using binary relationships, as shown in Figure 6.29b. Consider the alternative shown in Figure 6.29c. Discuss the relative mertis of these two alternative representations of a ternary relationship by binary relationships.

---

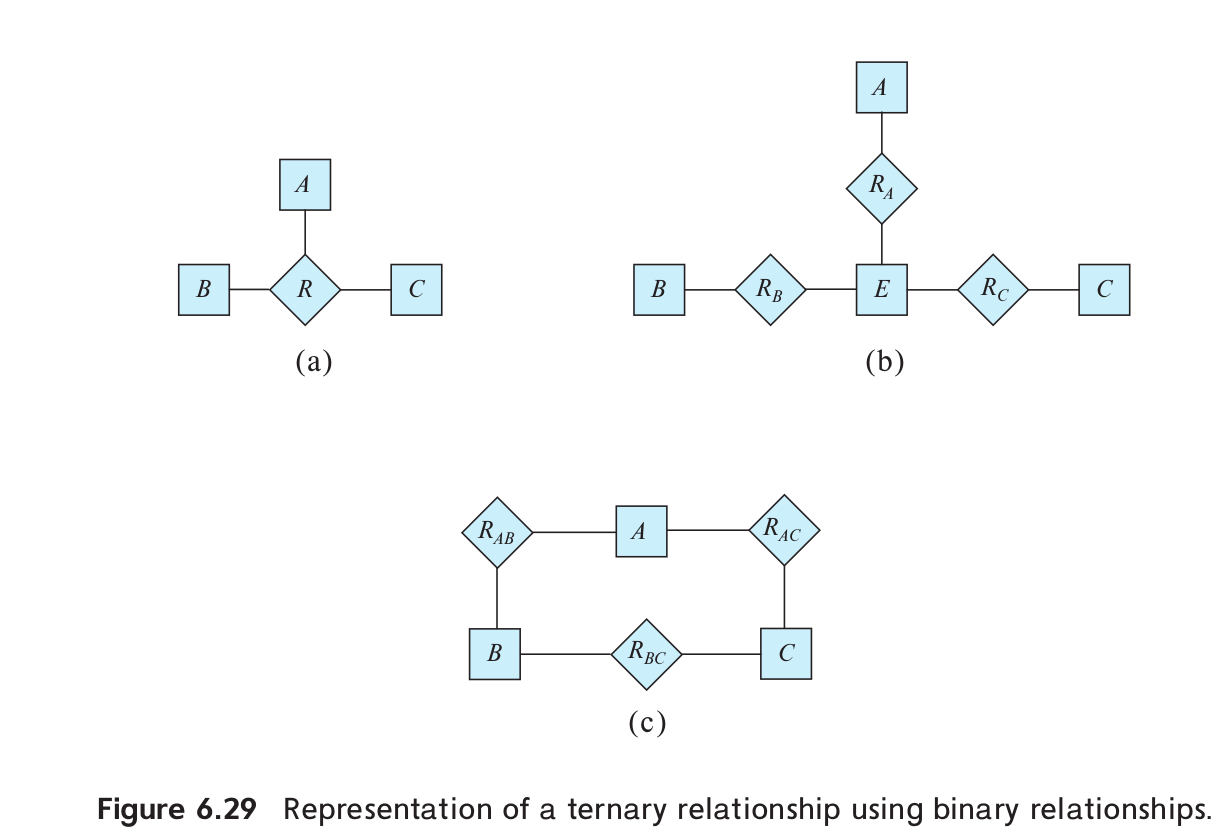
For Figure 6.29b to represent a ternary relationship, all relationship sets \(R_A\), \(R_B\), and \(R_C\) need to be many-to-one relationships, with a total participation from entity set \(E\).

Let \((a,b,c)\) in \(R\) (the ternary relationship in the above figure). Then we insert

• \((a,b)\) in \(R_{AB}\)
• \((b,c)\) in \(R_{BC}\)
• \((c,a)\) in \(R_{AC}\)

TODO: This answer needs more explanation.